LeetCode-142. Linked List Cycle II

发表于 分类于

问题描述

Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail’s next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.

Do not modify the linked list.

Example :

1
2
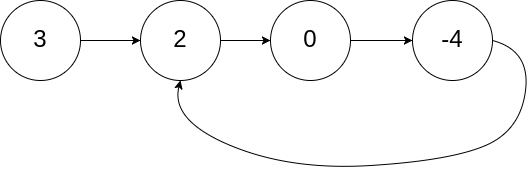
3
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

Constraints:

  • The number of the nodes in the list is in the range [0, 104].
  • -105 <= Node.val <= 105
  • pos is -1 or a valid index in the linked-list.

解答

通过快慢指针的方法可知，如果链表中有环，那么快慢指针一定会相遇，假设头节点到环入口节点的距离为x，环入口节点到相遇节点的距离为y，相遇节点到入口节点的距离为z，快慢指针分别在环中移动m和n圈后相遇，那么存在如下数学关系：

1
2
3
4
快指针走的步数 = x + m(y + z) + y
慢指针走的步数 = x + n (y + z) + y
x + m(y + z) + y = 2(x + n(y + z) + y)
(m - 2n)(y + z) = x + y

y + z即为环的长度，x + y为头节点到相遇节点的长度，两者之间时整数倍的关系，那如果安排前后两个指针，前面的指针从头节点出发，后面的指针从相遇节点出发，两者一起往前遍历，两者一定会重新在相遇节点相遇，往前倒推，环入口节点到相遇节点之间是两个指针一起经过的，那两者第一次相遇的节点就是环入口节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/*
 * @Description: 找到链表中环的入口节点
 * @Author: libk
 * @Github: https://github.com/libk
 */
/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} head
 * @return {ListNode}
 */
const detectCycle = function(head) {
  let slow = head
  let fast = hasCycle(head)
  if (fast === null) {
    return null
  }
  while (slow !== fast) {
    slow = slow.next
    fast = fast.next
  }
  return slow
}

function hasCycle (head) {
  if (head === null) {
    return null
  }

  let fast = head
  let slow = head
  while (fast !== null && fast.next !== null) {
    fast = fast.next.next
    slow = slow.next
    if (fast === slow) {
      return slow
    }
  }
  return null
}